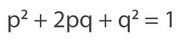The nice thing about models is that they allow you to do "what if" experiments on paper to assess how a system will behave under particular conditions. In population genetics, this can be extremely useful, because you can test different breeding strategies without having to actually produce many litters of puppies.
For example, let's say that a new genetic disorder has been discovered in your breed that is caused by a recessive mutation (we'll call it a), so individuals that are homozygous for the mutation (aa) are identified because they are "affected". To keep it simple, we'll say that affected animals can be easily identified at birth. Breeders will understandably want to eliminate the mutation from the breed, so they begin a rigorous program of removing all affected animals from the breeding population. How long will it take to eliminate the mutation from the breed?
We can use the Hardy-Weinberg equation to address this question:
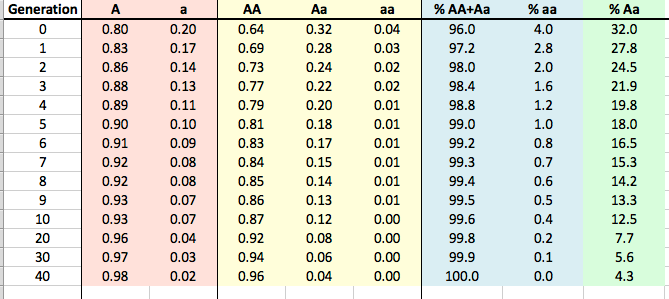
I've made this little table using the Hardy-Weinberg equation -
If we know the frequency of aa is 0.04 (= q x q; in the table above as the 0 generation aa in yellow), then the frequency of a (= q) must be the square root of 0.04, or 0.2 (= 20%; in the table above as the 0 generation a in red).
If 20% of the alleles in the population are a, then 80% must be A (in red for generation 0).
With this information we can fill in AA (as p x p; or, 0.8 x 0.8 = 0.64) and likewise Aa (as 2pq, or 2 x 0.8 x 0.2).
So, we now have both the gene frequencies and genotype frequencies in our population when the mutation is discovered. And, since we know that our mutation is recessive, we know that Aa will have the same phenotype (i.e., appearance) as AA, so we can also compute the phenotypes in the population (blue in the table above).
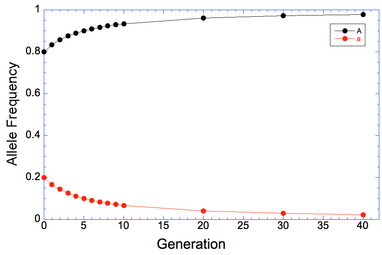
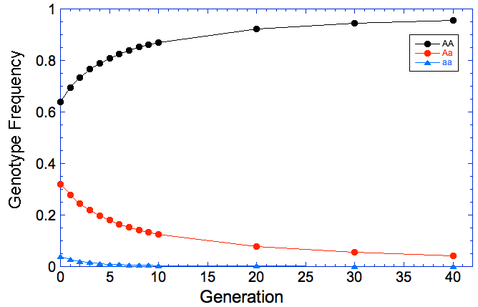
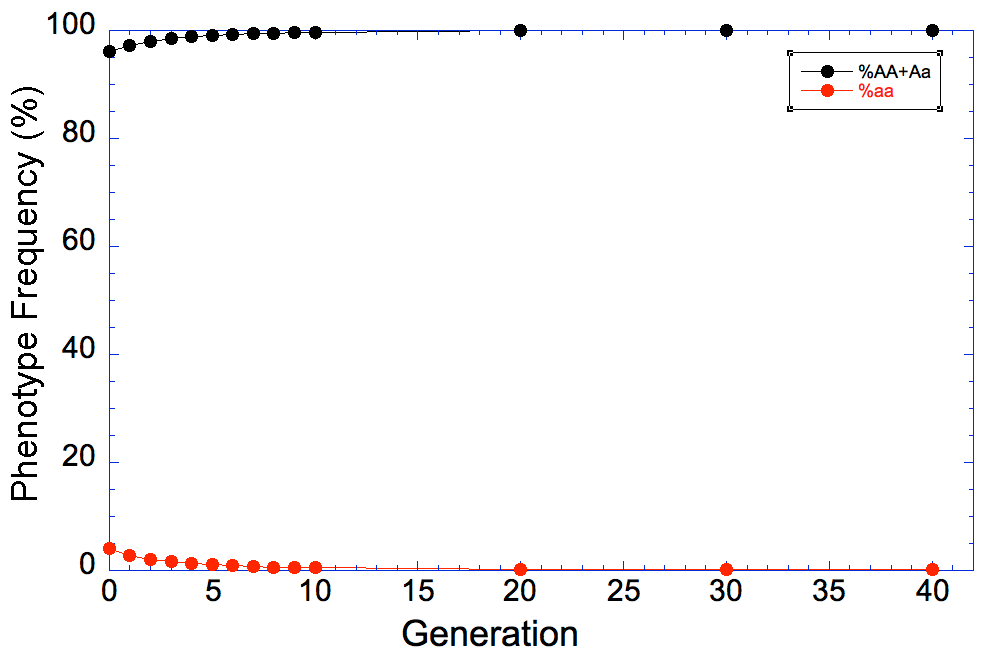
So now we want to see how long it will take to remove the mutation from the population if we remove all of the aa animals every generation. I've filled in the results in this table for generations from 1 to 40, and I've graphed the results below to make it easier to see what happens.
| The reason, of course, is that we are only selecting against the affected animals because we can recognize them by phenotype; animals that are carriers can't be detected, and when two carriers are bred they will produce affected offspring. We will reduce the carrier frequency through selection, but even after generations of strong selection against affected animals, we will still have carriers in the population and therefore the risk of producing affected animals. |
Go back to the table above, and look at the column in green. This is the percentage of the population each generation that would be carriers. Gosh, we would be throwing out more than 30% of the entire breed population for the first two generations, and another 20% or more for several generations after that (remember we're throwing out aa as well).
That's a LOT of dogs - and their genes - to eliminate, just to deal with that one nasty mutation. It's hard to imagine that you could do this without having serious consequences to the gene pool of the breed. Have a look at this chart of the biochemical steps that need to occur for proper energy metabolism. (Here's a tiny bit of it, just to give you an idea. If you've had some biology, you might remember that circular reaction, which is the Krebs cycle. It's too small to read, don't even try; look at the big version at the link above.)
It seems obvious that just tossing random genes out of the gene pool could get you into some trouble. Unfortunately, many breeds have done exactly this. Time and time again, a genetic disorder popped up suddenly out of nowhere, breeders decided to manage it by eliminating all dogs with the gene, both affected and carriers, and they decimated their gene pool. Then invariably some other, previously unknown mutation starts causing problems, and the purge cycle begins again. This isn't genetic management. This is breed suicide. But it happens over and over. And it might not be an overt policy to eliminate carrier animals, but if people refuse to breed from them, the effect is the same - eventually, it's a genetic catastrophe that breeders will be unable to reverse.
The original point here was to look at how we can use a simple model like the Hardy-Weinberg equation to see what might happen under certain conditions. We could elaborate on a simple model like this, and for instance add into consideration that breeding is not random apart from the mutation we're trying to get rid of, but instead there is some level of deliberate inbreeding. We could see how a specific rate of inbreeding would affect allele and genotype frequencies in the population over time, and what it would mean to our efforts to manage a damaging allele. Population geneticists now have sophisticated software that allows them to model breeding strategies to determine the most effective way to reach a certain goal, or to determine how long it would take a population to reach a certain size, or how the frequency of a genetic disease would change over time. The permutations are infinite. But at the core of all of these population genetic models is the Hardy-Weinberg law that describes how gene frequencies vary in populations.